Update: I made a video on this https://www.youtube.com/watch?v=cuZ99u7OSZE
I was reading about quaternions, so I decided to make a simple Quaternion library and visualizer in C++ to better understand them.
If you know what a complex number is, a quaternion is fairly similar. It is essentially a complex number with 3 imaginary components instead of one. I wanted to plot quaternions on a 2D graph to make visualizing quaternion equations easier to understand. Quaternions are often used to model 3D rotations. I first heard about them a few years ago when I was volunteering in a biophysics lab. One of the “killer features” is that they prevent gimbal lock, a major problem with modelling 3D rotations.
Using Complex Numbers for 2D Rotation
If you don’t know how complex numbers can be used to model 2D rotations, here is a quick recap. Consider the number \(\frac{\sqrt{2}}{2} (1 + i)\). The argument is \(\phi = 45^{\circ}\). If you square it, \((\frac{\sqrt{2}}{2} (1 + i))^2 = i\), which has \(\phi = 90^{\circ}\).
In summary:
$$\frac{\sqrt{2}}{2} (1 + i), \phi = 45^{\circ}$$ $$(\frac{\sqrt{2}}{2} (1 + i))^2, \phi = 90^{\circ}$$ $$(\frac{\sqrt{2}}{2} (1 + i))^3, \phi = 130^{\circ}$$ $$(\frac{\sqrt{2}}{2} (1 + i))^4, \phi = 180^{\circ}$$
Similarly, dividing will rotate clockwise, instead of anticlockwise.
Multiplying or dividing any complex number \(x\) by a number \(z, |z| = 1\), will rotate \(x\) by the argument of \(z\).
Using Quaternions for 3D Rotation
Quaternions work similarly for 3D rotations as complex numbers do for 2D rotations. Multiplying a quaternion will rotate an object, and dividing will rotate it back to the initial position.
Visualizations
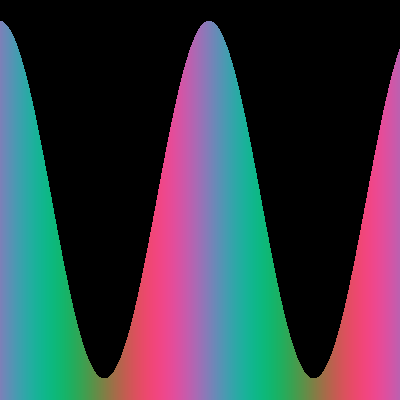
In this project, I plot a vector of quaternions on a two dimensional grid. The X axis reperesents the element in the quaternion vector. The Y axis represents the versor value of the real component of each quaternion. For the red, green, and blue values of each pixel, I used the values of the imaginary components of the versors. for instance, the unit quaternion would be gray (255/2 for each imaginary component). Negative values go to 0, positive values go to 255.
Adding complex components
In the picture below, I started with the quaternion \(-1 - 1k\), and added \(0.02i\) for every element in the size 400 quaternion vector.

Rotating numbers via multiplying by a constant
This one is more interesting - I am rotating the \(-1 + 0.5k\) quaternion by the \(0.999550 + 0.029987i\) quaternion. Notice that the rotation quaternion is a versor (it has a norm of 1). Since it’s nearly entirely a real versor, it rotates slowly around both the real and complex components, which is why the below image is sinusoidal in the Y axis and in color space (it rotates through colours) !